Click on image for full size
Original animation by Windows to the Universe staff (Randy Russell).
Eccentricity of an Orbit
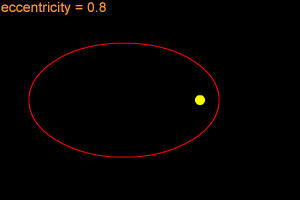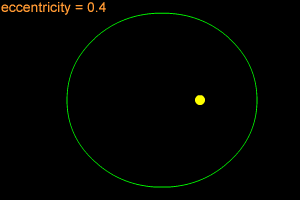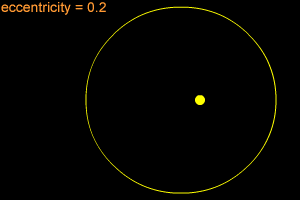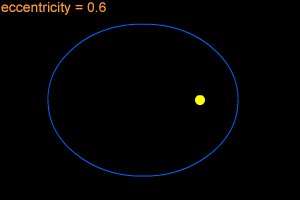
Most objects in orbits move along an elliptical path. An ellipse is a shape that can be thought of as a "stretched out" circle or an oval. An ellipse can be very long and thin, or it can be quite round - almost like a circle. Mathematicians and astronomers use a quantity named "eccentricity" to describes how nearly circular (or not) an ellipse is.
An ellipse with a small eccentricity, like 0.1 or 0.2, is almost as round as a circle. A long, thin ellipse might have an eccentricity of 0.8 or 0.9. The eccentricity of an ellipse must always be less than one, but it can be very, very close to one - like 0.99, 0.999, or even larger!
A circle has an eccentricity of zero. A circle is considered a special type of ellipse, in the same way that a square is considered a special type of rectangle.
The eccentricity of Earth's orbit is very small, so Earth's orbit is nearly circular. Earth's orbital eccentricity is only 0.0167. Mars has a somewhat larger orbital eccentricity of 0.0935. The orbits of Mercury and Pluto have the largest eccentricities of planetary orbits in our Solar System; 0.2056 for Mercury and 0.2488 for Pluto. Comets often have extremely eccentric orbits. Halley's Comet, for instance, has an orbital eccentricity of 0.967!
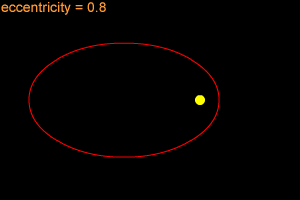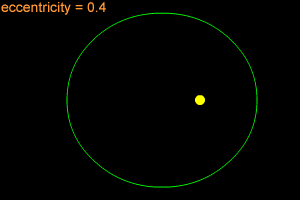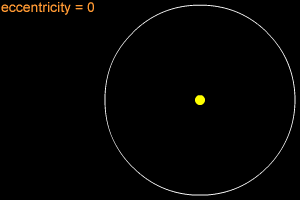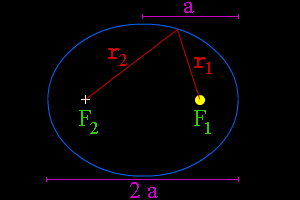
When an object follows an elliptical path while orbiting a larger object, the larger central body is not at the center of the ellipse. Instead, the central body is at a point called a focus of the ellipse which is offset from the center. The larger the eccentricity, the more the focus is offset from the center. This means that the orbiting object moves closer towards and further away from the central body during the course of an orbit. The close point in an orbit around the Sun is called the perihelion; the far point is called aphelion. More eccentric orbits lead to greater differences in perihelion and aphelion distances. Earth is only 3% further from the Sun at aphelion than it is at perihelion, while Pluto's aphelion distance from the Sun is 66% greater than its perihelion distance.
The force of gravity dictates that a small body moving in the presence of a more massive body (such as a planet, asteroid, or comet orbiting the Sun; or a satellite orbiting Earth) will follow a trajectory with a shape called a "conic section". Image slicing a three-dimensional cone with two-dimensional plane at various angles; the resulting "slices" are conic sections. Circles and ellipses are conic sections; so too are parabolas and hyperbolas. A circle has an eccentricity of zero. An ellipse has an eccentricity between zero and one. A parabola has an eccentricity of exactly one, while hyperbolas have eccentricities greater than one. Parabolic and hyperbolic trajectories are not orbits; they only result in a single close pass by the parent body, while orbits result in repeated close approaches. Some comets (such as Halley's) follow elliptical orbits that bring them back to the inner solar system again and again, though sometimes only after long intervals (75 years for Halley's). Other comets are on hyperbolic trajectories, and only visit the inner solar system once before being flung off into interplanetary space, never to return.