Solar Radiation at Earth
The Sun emits a tremendous amount of energy, in the form of electromagnetic radiation, into space. If we could somehow build a gigantic ball around the Sun that completely enclosed it, and lined that ball with perfectly efficient photovoltaic solar panels, we could capture all of that energy and convert it to electricity... and be set in terms of Earth's energy needs for a very long time. Lacking such a fanciful sphere, most of the Sun's energy flows out of our solar system into interstellar space without ever colliding with anything. However, a very small fraction of that energy collides with planets, including our humble Earth, before it can escape into the interstellar void. The fraction of a fraction that Earth intercepts is sufficient to warm our planet and drive its climate system.
At Earth's distance from the Sun, about 1,368 watts of power in the form of EM radiation from the Sun fall on an area of one square meter. Yes, these are the same watts we use to describe the energy usage of light bulbs and other household appliances. If Earth were closer to the Sun, as, for example, the planet Mercury is, the number of watts per square meter (W/m2) would be greater. If Earth were further from the Sun, the W/m2 value would be lower. Recall our hypothetical gigantic ball surrounding the Sun. Whatever its size, it would capture all of the Sun's energy; but a larger ball would have that energy spread over a larger inside surface area, and would thus have a lower W/m2 value; whereas a smaller ball would have a smaller surface and thus a greater W/m2 value. The surface area of a sphere varies as the square of the radius of the sphere; so the energy per unit area received varies inversely as the square of the distance from the Sun. A planet situated 1/2 as far from the Sun as is Earth would be scorched by 4 times as much energy from the Sun (5,472 W/m2). A planet twice as far from the Sun as is Earth would be feebly warmed by just 1/4th as much radiation (342 W/m2). So our planet's distance from the Sun is the first key factor influencing the energy we receive, and thus the behavior of our climate.
If Earth were a flat, one-sided disk facing the Sun... and if it had no atmosphere... every square meter of Earth's surface would receive 1,368 watts of energy from the Sun. Although Earth does intercept the same total amount of solar EM radiation as would a flat disk of the Earth's radius (see figure below), that energy is spread out over a larger area. The surface of a sphere has an area four times as great as the area of a disk of the same radius. So the 1,368 W/m2 is reduced to an average of 342 W/m2 over the entire surface of our spherical planet. Another way to think of this reduction is to realize that half of Earth's surface (the night side) is in the dark and thus receiving no solar energy at a given moment, while areas near the edges of the planet (near the poles and around dusk and dawn) are receiving reduced amounts of energy per unit area.
The spherical Earth actually "intercepts" the same amount of incoming solar EM radiation as would a flat disk of the same radius, as shown here. However, the average energy per unit area of Earth's surface is one quarter of that which would strike a flat disk, once we factor in our spherical planet's larger surface area and the fact that half of it is in the dark at a given time. |
Note that the values for average solar insolation (the term scientists use for the solar EM energy delivered to an area) reaching Earth that have been discussed so far are at the top of the atmosphere. As you can imagine, as sunlight passes through our atmosphere, some of it is scattered and absorbed, reducing the amount that actually reaches the ground. We'll take up that issue in a bit, but for now we'll continue to simplify our discussion by assuming an airless Earth.
Whenever you glance up at the full moon, you get an eyeful of the subject of our next topic. Unlike the Sun which generates light itself, the Moon does NOT produce light. The moonlight we see on Earth is reflected sunlight. So, not all of the energy in the form of sunlight that reaches the Moon stays there; some is reflected back into space. Likewise, not all of the energy from the Sun that reaches Earth sticks around here to warm our planet; some is reflected back into space. Take a look at these two images of our planet that were captured by the Galileo spacecraft in December 1990:
Obviously, quite a bit of the sunlight that reaches Earth is reflected back into space. The white clouds that cover much of both images, and the white ice of Antarctica, both reflect most of the sunlight that falls upon them. You can also see how the oceans, the deserts of northern Africa, and the jungles of central Africa and of South America reflect or absorb varying amounts of sunlight.
Albedo
Astronomers use a quantity called "albedo" to describe the degree to which a surface reflects light that strikes it. An extremely reflective surface that doesn't absorb any of the light that hits it would have an albedo of 1, while a surface that reflects none of the light that hits it (and that would thus appear pitch black under any illumination) would have an albedo of 0. Fresh snow has an albedo somewhere around 0.8 or 0.9. Forests have albedos near 0.15, while the albedo of desert sands is roughly 0.4. Climate scientists also employ the concept of albedo, though they often express it as a percent; thus they would say that snow has an albedo of 80% to 90%, while the albedo of a forest would be around 15%.
The albedo of a planet (or a locale on it!) clearly affects the ability of that planet to absorb sunlight, thus converting it to heat that can warm the planet and drive its climate. Earth's overall average albedo is about 0.31. Oceans and forests are quite dark, while deserts are lighter, and clouds, snow, and ice are very bright. Without clouds our planet's albedo would be around 0.15, so clouds roughly double Earth's albedo.
Balancing Equations: Earth's "Theoretical" Temperature
We now have nearly all of the tools in hand to estimate what the surface temperature of a simplified (that is, lacking an atmosphere and averaging the albedo over the whole planet) Earth "should be". Here's how that calculation goes. We assume Earth is in a steady state, neither warming or cooling rapidly. Our planet is obviously receiving an influx of energy (those 342 W/m2 of solar EM radiation); so, to stay in balance, it must be getting rid of just as much energy (otherwise it would heat up rapidly). So how is Earth shedding energy? Any object that has a temperature above absolute zero emits electromagnetic radiation. Wave your hand above a burner atop an electric stove; even if it isn't hot enough to glow red with visible light, you'll clearly feel the heat from its infrared emanations. Objects much less warm than a stovetop, including our planet, also emit EM radiation, generally in the infrared range. It turns out that there is a mathematical relationship between the temperature of an object and the amount of energy it radiates (the Stefan-Boltzmann law). We'll use that relationship to balance the energy input from the Sun, and thus to calculate the "expected" surface temperature for Earth.
This next section delves into the math of that energy balance calculation. These calculations are supplied for those who are interested in them, but this is not required knowledge for this course. Feel free to skim over this section, and to take our word for it with regards to the results if you are not interested in the details of the mathematics.
We need to balance: Total power absorbed = Total power emitted | |||||||||||||||||
Total power absorbed
[Note: we use the "Earth as a disk" assumption mentioned earlier to calculate the "area of planet facing Sun".] | Total power emitted
Where s is the Stefan-Boltzmann constant, with a value of | ||||||||||||||||
When we set the power absorbed and the power emitted equations equal to each other, p and the Earth's radius term cancel out, so we are left with: 1,368 W/m2 x (1 - albedo) = 4 x s x T4 Or, using Earth's average albedo of 0.31 and solving for T: T4 = [1,368 W/m2 x (0.69)] / 4s Which yields T = 254 K ( = -19° Celsius = -3° Fahrenheit) | |||||||||||||||||
This simplified model of Earth yields an average global temperature for our home world of 254 K (or -19° Celsius or -3° Fahrenheit). Such a planet would be a chilly place indeed; most or all of the water on Earth would be frozen if this were indeed the temperature of our world. In reality, Earth's overall average temperature is roughly +15° C (or +59°F or 288 K). As we'll see in a bit, our atmosphere makes this planet a much more comfortable place to live!
Earth's "Theoretical" Temperature - What if?
Let's take a look at some "what if?" scenarios to see how Earth's "theoretical" temperature would change if the amount of solar energy we receive was altered or if our planet's albedo changed. The interactive below allows you to adjust these two parameters and see how Earth's "theoretical" temperature would respond. Drag the sliders for "Sun's brightness" and for "Earth's albedo" to alter those values, and see how Earth's temperature changes in as a result. The interactive does the same calculation we just walked through above to generate the temperature it reports. There are some suggestions below of scenarios to try out. (Note: the popup menu for changing the "Sun's brightness" values between W/m2 and percent isn't working quite yet; please ignore that!)
|
|
Here are some scenarios to play around with:
- Recall how scientists believe the Sun was only about 70% as bright early in its history as it is today ("The Faint Young Sun Paradox"). Try setting the "Sun's Brightness" to something like 958 W/m2 (70% of 1,368 W/m2) to see how that would impact Earth's temperature.
- Earth without clouds would have an albedo of about 0.15; how would that affect its temperature?
- During ice ages, much more of our planet was covered with highly reflective snow and ice. Some scientists think that there may have been periods early in Earth's history when our planet was gripped by severe ice ages that froze over all or nearly all of Earth ("The Snowball Earth Hypothesis"). What would a global average albedo of 0.8 or 0.9 do to Earth's temperature?
- What if Earth was a desert planet? Or an ocean planet? Or entirely covered with forests? Check out the tables below that provide approximate values for the albedos of these types of surfaces; plug them into the interactive; and see how Earth's temperature might respond.
Albedo values for various surfaces (expressed as percentages)From various sources (that don't entirely agree with each other - take these with a grain of salt!). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Source: book "Earth's Climate: Past and Future" by William F. Ruddiman; Table 2-1 on p. 23 |
Source: an online lesson/activity writeup from NOAA called "Canned Heat". |
Source: diagram from a natural sciences course at U. of Arizona. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Finally, we'll briefly touch upon two more "odds-and-ends" topics related to the heating of Earth by the Sun.
Energy per Unit Area and Sun Altitude Angle - Latitude and Seasons
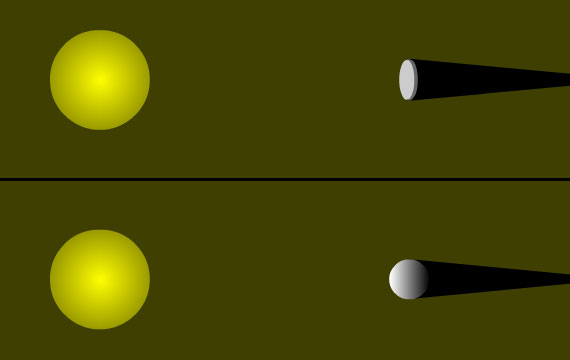
You've probably noticed that when the Sun is "low in the sky" its "warming power" is diminished. Near sunrise or sunset, or in the dead of winter when the Sun barely creeps above the horizon, our neighborhood star provides us with less heat than it does when it "beats down on us" from almost directly overhead at noon on a summer day. Part of this effect is due to our atmosphere; the Sun's rays pass through more air on their way to us when the Sun is low in the sky than when it is directly overhead, and some of the Sun's energy is scattered or absorbed by our atmosphere. However, this reduced heating is largely controlled by basic geometry that has nothing to do with the atmosphere.
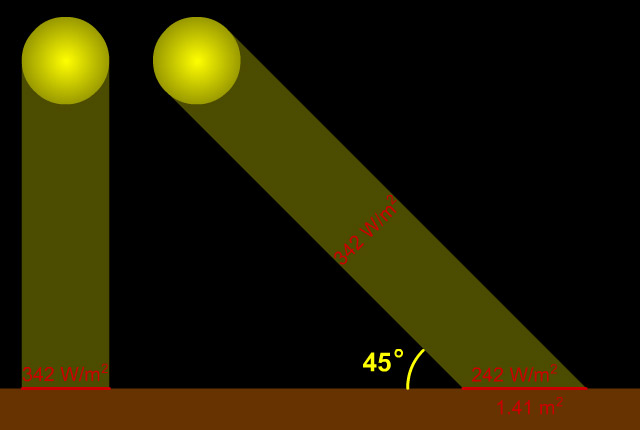
When the Sun is directly overhead, its light (and energy) is concentrated upon the smallest possible surface area of the ground that it can strike (and be absorbed by). However, when the Sun is lower in the sky, its light/energy strikes the ground obliquely, and is thus spread out over a larger area. An oft-employed analogy for this situation is of two identically sized pats of butter being spread over a smaller and larger slice of bread. The amount of energy per unit area is thus diluted; more so the lower in the sky the Sun appears. The diagram below illustrates this concept.
When the Sun is directly overhead, its rays strike Earth perpendicular to the ground and so deliver the maximum amount of energy. When the Sun is lower in the sky, a sunbeam strikes the ground at an angle (in the example above, 45°) and so its energy is "spread out" over a larger area... thus "diluting" its energy. In this example, the energy is spread over an area of 1.41 square meters (instead of 1 square meter when the Sun is directly overhead), so the energy per unit area is reduced from 342 W/m2 to 242 W/m2 (342 ÷ 1.41 = 242). |
This effect impacts solar radiation's ability to heat our planet in two key ways. Regions of our planet at high latitudes (near the North and South Poles) receive far less concentrated solar energy than do regions at low latitudes (in the tropics near the equator). And... surprise, surprise... Earth is much warmer in the tropics than it is in the polar regions! The polar regions are, in fact, hit by a bit of a double whammy in terms of cooling... the low Sun angle means they receive less solar energy... and their high albedo due to extensive ice and snow cover means that they reflect away much of the solar energy that does reach them! The interactive below illustrates how solar energy intensity per unit area varies with latitude.
|
|
Our seasons also influence how much solar radiation strikes a square meter of ground in a given place on the planet's surface at a given time of year. The Sun is "higher in the sky" in the summer and "lower in the sky" in winter. Thus basic planetary heating patterns change seasonally throughout the year, influencing climate. In the interactive below, click on the (Northern Hemisphere) "Summer" and "Winter" buttons and check out the "View from Sun" to get a sense of the change in the solar radiation received at a given location on Earth from season to season.
|
|