Click on image for full size
Original animation by Windows to the Universe staff (Randy Russell).
Elliptical Orbits
When one object is in orbit around another object, the orbit is usually an elliptical orbit. For example, all of the planets in our Solar System move around the Sun in elliptical orbits. An ellipse is a shape that can be thought of as a "stretched out" circle or an oval.
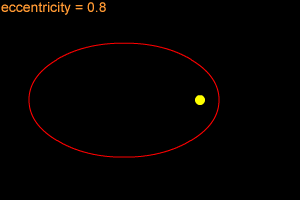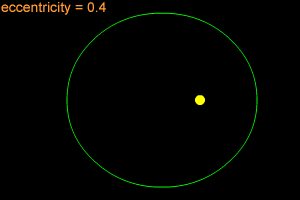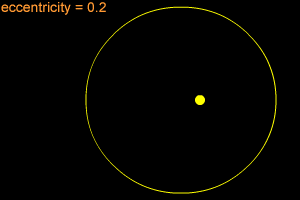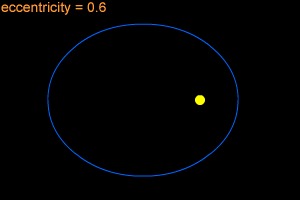
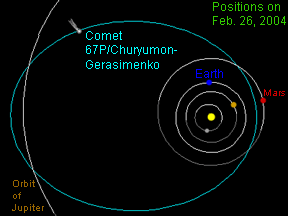
An ellipse can be very long and thin, or it can be quite round - almost like a circle. In fact, a circle is considered a special type of ellipse, in the same way that a square is considered a special type of rectangle. "Eccentricity" is the technical term that mathematicians and astronomers use to describes how nearly circular (or not) an ellipse is. An ellipse with a small eccentricity, like 0.1 or 0.2, is almost as round as a circle. A long, thin ellipse might have an eccentricity of 0.8 or 0.9. A circle has an eccentricity of zero. The eccentricity of an ellipse must always be less than one, but it can be very, very close to one - like 0.99, 0.999, or even larger!
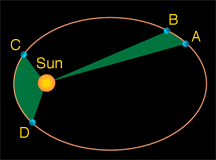
When an object is in an elliptical orbit around another larger (more massive) object, the larger object is not at the center of the ellipse. There are two points inside of an ellipse called the "foci" ("foci" is the plural form of "focus"). The larger objects is at one of the two foci. For example, the Sun is at one of the foci of Earth's elliptical orbit. If the eccentricity of an ellipse is large, the foci are far apart. If the eccentricity is small, the foci are close together. In the extreme case of a circle, with an eccentricity of zero, the foci merge together into a single point - the center of the circle.
Objects moving in elliptical orbits move fastest when they are closest to the central body, and most slowly when they are furthest from the central body. Johannes Kepler realized this and stated it in his Second Law of Planetary Motion. The points of closest approach (and fastest motion) and furthest separation (and slowest motion) between the two objects have been given special names. For planets (or asteroids, comets, or spacecraft) orbiting the Sun, these points are called perihelion (close) and aphelion (far).
Strictly speaking, two objects actually orbit each other, and it is the center of mass of the two-body system that they orbit around. In many actual cases, when one object is much larger (more massive) than the other, we are justified in making the approximation that the smaller object orbits the larger, and that the large object is at a focus of the orbital ellipse. For common cases like planets orbiting the Sun or the Moon orbiting Earth, this approximation is very close to the truth. However, there are some systems for which this approximation is not so good. Two such examples are the stars in a binary pair and duos of asteroids that orbit one another.
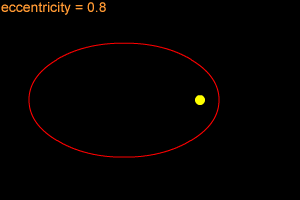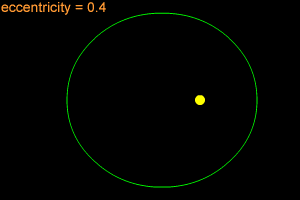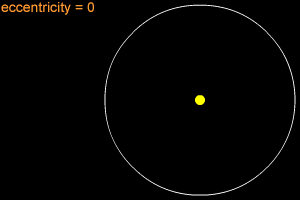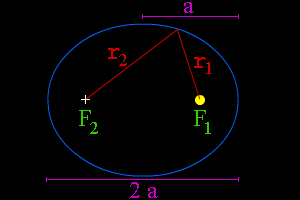
Let's take a look at the mathematical definition of an ellipse. First, place two points on a plane; these will be the foci of the ellipse. Now, pick a distance that is larger than the distance between the two foci. We'll call that distance "2a", for reasons that will become clear in a minute. Let's say that a point "P" is on the ellipse. The distance from one focus (F1) to P is r1; the distance from the other focus (F2) to P is r2. A point P will be on the ellipse if and only if the sum of its distances from the two foci adds up to 2a; that is:
r1 + r2 = 2a
If we draw a line along the long axis of the ellipse, through its center and both foci, the length of the ellipse along that axis will be 2a. The distance from the center of the ellipse to either of its ends along that axis equals a. The value "a" is given a special name; it is called the "semi-major axis" of the ellipse.
You can draw an ellipse using a string and two thumbtacks. Put a piece of paper on some cardboard, and stick the two thumbtacks into the paper. The locations of the thumbtacks will be the foci of the ellipse. Attach one end of a piece of string, that is longer than the distance between the tacks, to one tack; attach the other end of the string to the other tack. Now, stretch the string out to the side and draw along it with the pencil, always keeping the string taut. You'll need to move the pencil at least once to draw both halves of the ellipse. By varying the length of the string, you can draw different ellipses with different eccentricities. The string's length is 2a, the length of the major axis of the ellipse.