This picture shows Pluto (left) and its big moon Charon (right). Notice how big Charon is compared to Pluto. Notice how close Charon is to Pluto. This picture was taken by the Hubble Space Telescope in 1994.
Click on image for full size
Image courtesy Dr. R. Albrecht (ESA/ESO Space Telescope European Coordinating Facility) and NASA.
Charon - Pluto's biggest moon
Charon is a moon of Pluto. Pluto has
moons. Charon is much larger than Pluto's other moons. James Christy discovered
Charon on June 22, 1978.
Charon is nearly as big as Pluto. Some astronomers call Pluto and Charon a
"double planet". Charon is also
very close to Pluto. Because Charon is so close, it goes around Pluto fast.
It only takes Charon a little more than six days to orbit Pluto.
Did you know that we can only see one side of our Moon from Earth? That's
because the Moon spins around in exactly the same amount of time it takes it
to orbit Earth. The same thing is true for Charon and Pluto. Someone on Pluto
could only ever see one side of Charon. Now here's the really strange part.
Pluto also spins exactly as fast as Charon. So on one side of Pluto, Charon
is always up in the sky. A person on the other side of Pluto would never see
Charon at all!
Charon is made of rock and ice, like Pluto. Some astronomers think Charon
formed when a large object
crashed into Pluto. That is a lot like how scientists
think Earth's moon formed. Other scientists aren't quite so sure that Charon
was formed that way.
Charon is named after a character from Greek
mythology. Charon was the ferryman
of the dead. He took people who had just died across a river in a boat. He took
them to Hades, the underworld. Hades was also the name of the god of the underworld.
In Roman mythology, Hades
was called Pluto.
You might also be interested in:

Pluto is a frigid ball of ice and rock that orbits far from the Sun on the frozen fringes of our Solar System. Considered a planet, though a rather odd one, from its discovery in 1930 until 2006, it was
...more
Pluto has // Call the moon count function defined in the document head print_moon_count('pluto'); moons. One of the moons is very large. The large moon is named Charon. The other two moons are fairly small.
...more
Of all the planets and moons in the solar system, Pluto and Charon are the two which resemble each other the most closely. They are almost the same size, and they are very close together. They are so
...more
Pluto is so far away, and has never been explored. Questions to answer about Pluto include the following: What are the geologic features of the surface. (pictures of the surface) If there are bare spots,
...more
It may seem hard to believe that Pluto could have an atmosphere because it is so cold at 39 AU, where Pluto is found, but it does. Because there are times when Pluto is closer to the sun than is Neptune
...more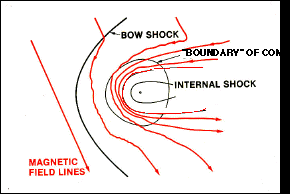
No one knows whether or not Pluto has a magnetosphere. Scientists were very surprised to find that Jupiter's icy moon Ganymede had a magnetosphere because it is hard to explain how an icy body can develop
...more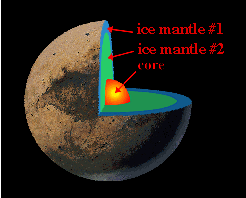
The diagram to the left shows a cutaway of the possible interior structure of Pluto. The composition of Pluto is mostly ice, therefore there is probably a small core of some rocky material buried inside,
...more













