Click on image for full size
Windows to the Universe original artwork by Randy Russell.
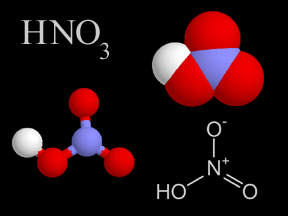
Nitric Acid - HNO3
Nitric acid is a colorless, corrosive liquid and a toxic acid which can cause severe burns. Nitric acid consists of nitrogen, oxygen, and hydrogen atoms. Nitric acid, in its gas phase, is present in very small quantities in Earth's atmosphere.
Nitric acid is one of the components of acid rain. Clean air has very little nitric acid in it, but some types of pollution generate this acid. For example, the engines of motor vehicles produce nitrogen oxide compounds when they burn their fuel. Nitrogen dioxide (NO2) from car exhaust turns into nitric acid when it mixes with water vapor. This mixture falls from the sky as acid rain.
The Persian alchemist Jabir ibn Hayyan first synthesized nitric acid around 800 A.D. Nitric acid is used in the manufacture of explosives, including nitroglycerin and trinitrotoluene (TNT). Nitric acid is also involved in the production of chemical fertilizers such as ammonium nitrate. Because it is such a strong acid, nitric acid is also widely used in industry for cleaning and etching metal, electroplating, refining, photoengraving, and in jewelry manufacturing. It is also used as an oxidizer in some liquid-fueled rockets.
Humans generate nitric acid wherever very high temperature combustion takes place in the atmosphere in the presence of nitrogen, oxygen and water. The exhausts of incinerators or other chemical plants and the tailpipes of cars and trucks are common sources. Because it is so reactive with other compounds, nitric acid does not remain in Earth's atmosphere for long. Nitric acid reacts with gaseous ammonia to form particulate or aerosol nitrate, removing the nitric acid from the atmosphere within a few days of its creation.