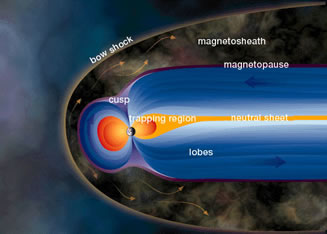
Charged Particle Motion in Earth's Magnetosphere
Drift Motion of Charged Particles
If a uniform electric field 
is
added the magnetic field 
the
charged particle experiences a force:
in addition to the magnetic force:
The total force on the particle is thus:
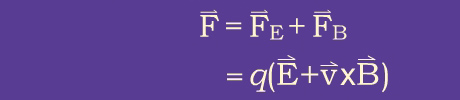
Only the electric force can do work on the particle since the magnetic
force is always perpendicular to the particle velocity. If both 
and are
perpendicular to ,
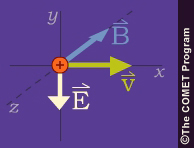
acceleration by the electric field changes the circular motion shown on the preceding page.
In the segment of its orbit when the particle is moving in the direction
of the electric force, it accelerates, and its gyroradius expands. When
it moving against the electric force, it decelerates and its gyroradius
contracts. These distortions of the gyroradius cause the particle to
drift in a direction perpendicular to both and .
Notice in the following animation how the velocity increases during the particle's downward swing, reaching its maximum at the base of the orbit. The veclocity vector has a rightward component during the half of the orbit when it is strongest, while it has a leftward component during the half when velocities are weakest. The net effect is a rightward drift.
|
|
These distortions of the gyroradius cause the particle to drift in a
direction perpendicular to both and .
The average drift velocity is given by:
This kind of drift can be induced by any effect that modifies a particle’s gyroradius over the course of its orbit.
