There are 6 main steps involved in calculating the circumference (and radius) of the Earth. Click on each step for full information. You may find our worksheet helpful in recording each step.

Step 1) Measure the length of the shadow cast by a gnomon at local solar noon.  For MYW, this will be done with your Partnership in each of three locations; United States of America, Chile, and Mexico. Report this online!

Step 2) Determine the angle of the shadow in each location, called the gnomon-sunbeam angle.

Step 3) Determine the "vertical angles" by combining (either adding or subtracting depending on the latitude) the gnomon-sunbeam angles at pairs of locations from your MYW Partnership.

Step 4) Determine the separation distance between measurement locations projected over the zenithal circle.  This can be found using the online distance calculator.

Step 5) Calculate the Earth’s circumference (and radius) using the vertical angle (step 3) and separation distance (step 4) between locations for each pair of locations.

Step 6) Average the Earth’s circumference (and radius) values for each pair of locations you calculated to get a final value for the Earth’s circumference and radius!  Report this online!

 

Step 1: Measure Shadow Length

Follow the steps as described as in the Measure section of this site or on the downloadable Activity Guide. Here are a few important notes:

Step 2: Determine the Gnomon-Sunbeam Angle

There are two ways to do this: using graph paper and a protractor, or using some basic trigonometry.

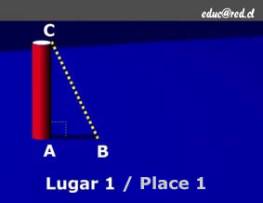
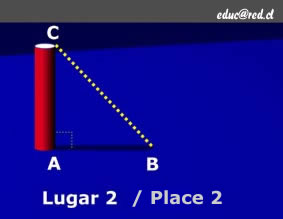
The two figures below show the geometry of a gnomon, sunbeam, and shadow in two different locations. We will refer to them throughout the following descriptions.

Gnomon figure 1

Figure 1

  

Gnomon figure 2

Figure 2

Using graph paper and a protractor

You will make a "scale model" of the gnomon and its shadow on a piece of graph paper, and use a protractor to measure the angle. You will need the following materials:

You will need your measurements of the height of your gnomon and the length of the shadow that was cast by the gnomon.

  1. Draw a line on the graph paper to represent the gnomon. Pick a scale that fits on your paper. You will need to use the same scale for your gnomon and for the shadow. For example, if your gnomon is one meter long (100 cm) and the line for it you draw on the graph paper is 20 cm long, your scale is 1/5th.
  2. Draw a line on the graph paper perpendicular to (at a right angle, 90, to) the gnomon line, extending from one end of the gnomon line. This line will represent the shadow. Use the same scale that you used when drawing the gnomon line. For example, using the example numbers from step 1 above, if the actual shadow was 45 cm long, the line representing it on the graph paper should be 9 cm (1/5th of 45 cm) long.
  3. Connect the tips of the gnomon line and the shadow line on the graph paper with a third, straight line. You should now have a triangle (a right triangle, in fact!).
  4. Look at figures 1 & 2 above. Label the corners of your triangle with the letters A, B, & C in the same way they are labelled in figures 1 & 2.
  5. Use your protactor to measure angle ACB.

Using basic trigonometry

Refer to figures 1 and 2 above. The goal is to find angle ACB. We know the length of the gnomon (or line segment AC) and the length of the shadow (line segment AB). We also know that the gnomon is vertical, so angle BAC is a right angle (90°).

We'll use the Greek letter phi (φ) to represent the size of angle ACB.

Trigonometry tells us that:

tan φ = AB / AC = (Length of shadow) ÷ (Height of gnomon)

Solving for angle ACB (or φ), we get:

φ = arctan (AB / AC) = arctan [(Length of shadow) ÷ (Height of gnomon)]

Example: If the gnomon is 1 meter (100 cm) high and the shadow is 20 cm long, we get:

tan φ = 20 cm / 100 cm = 0.2

φ = arctan (20 cm / 100 cm) = arctan (0.2) = 11.3 degrees

Step 3: Determine the "Vertical Angles" by Combining Pairs of Gnomon-Sunbeam Angles

To determine the size of Earth, we need angle measurments from two different places on the planet that are have at least moderately different latitudes. Once we have the angle measurements from two different locations, we need to combine those angles to get the "vertical angle" that we will use in further calculations. To combine the angles, we either add the two angles together or subtract one from the other. Whether we add or subtract angles depends upon whether the two places are in different hemispheres or the same hemisphere. (If you need the shadow measurements for your MYW Partners' locations, please either communicate with them online or use our data lookup tool.)

In the case of the Measure Your World project, most locations will be in Chile, Mexico, and the U.S.A.

Locations of Angle Measurements How to Calculate "Vertical Angle"
Chile and Mexico
φ Chile + φ Mexico
Chile and U.S.A.
φ Chile + φ USA
Mexico and U.S.A
φ USA - φ Mexico

Example:

Location φ (angle ACB)
Chile
37°
Mexico
23°
U.S.A.
42°
 
Location Pair
Vertical Angle
Chile and Mexico
60° = 37° + 23°
Chile and U.S.A.
79° = 37° + 42 °
Mexico and U.S.A
19° = 42 ° - 23°

Step 4: Determine the Separation Distance Between Measurement Locations Projected over the Zenithal Circle

When Eratosthenes used this method to find the size of Earth, he had several things going for him that made the calculation relatively easy. One of the two locations he used, the Egyptian town of Syene, is on the Tropic of Cancer... so the Sun was directly overhead there on the solstice, casting no shadow, and thus the angle of the gnomon's shadow was zero. The two locations Eratosthenes, Alexandria and Syene, have approximately the same longitude... Syene is almost due south of Alexandria. Finally, on the solstice, two places with the same longitude experience solar noon at the same time... further simplifying calculations.

In your case, we have provided you with a calculator that will determine the "correct" distance between two places at which you are making sun angle measurements. You will need to supply the calculator with the longitudes and latitudes of the two places your are comparing, and the times and dates when you made your sun angle measurements. The calculator will determine the "correct" distance between the two places.

Use this link to go to the distance calculator. Enter the locations (latitude and longitude) of each pair of places, and the time and date when you took the measurements. If you need the lat/lon, times and dates for your MYW Partners' measurements, please either communicate with them online or use our data lookup tool. You will need to enter the universal time (also known as GMT, Greenwich Meridian Time) at which this measurement took place. Please be aware of daylight savings time. You can use the following links to transform the reported local time into GMC:

http://sunearth.gsfc.nasa.gov/eclipse/SEhelp/TimeZone.html#UTC
http://wwp.greenwichmeantime.com/info/time.htm

Click the calculate button. The calculator will give you the "correct" distance between the two places; record this number - you'll use it in Step 5 below. Do this for each of the three pairs of places where your group is making measurements.

If you want to learn more about the reasons your calculation is more complex than the one Eratosthenes had to do, check out the links to videos below:

Step 5: Calculate Earth's Size for Each Pair of Locations

You now have all the information you need to calculate the circumference and radius of Earth based on the shadow angles you observed at two locations and the distance you just calculated between the two locations. The vertical angle you found in step 3 is the same as the angle, measured at Earth's center, between the two locations on the globe. You should now construct a simple ratio using your vertical angle, your distance between places, and the known number of degrees in a circle (360°) to determine the Earth's circumference. Let's define the following variables:

D and θ are known; you'll need to solve for C.

C / D = 360° / θ

So,

C = D x 360° / θ

Example: Suppose you found that the vertical angle, θ, was 60°; and that the distance, D, was 6,500 km. Your ration would be:

C / 6,500 km = 360° / 60°

... and your value for Earth's circumference would be:

C = D x 360° / θ = (6,500 km) x 360° / 60° = 39,000 km

You can calculate Earth's radius from the circumference by recalling that the circumference of a circle (or sphere) is 2π times the radius:

Radius = C / 2π

For the example above, the radius would be:

Radius = C / 2π = (39,000 km) / 2π = 6,207 km

Step 6: Average the Earth Size Calculations from 3 Locations to get the Final Value for the Earth's Size

You should do the calculations described in step 5 three times; once for each pair of locations (Chile & Mexico; Chile & USA; and Mexico & USA). Since it extremely unlikely that your mesurements were all perfect, the calculations will likely result in three different values for Earth's circumference. To get a single value of the Earth's cirucmference for your team, average the three circumference values.

Caverage = [CChile-Mexico + CChile-USA + CMexico-USA] ÷ 3

Report your final calculation of the Earth's circumference and radius to us!

Example: Suppose you had the following three values for Earth's circumference:

Caverage = [39,700 km + 40,200 km + 38,900 km] ÷ 3 = 118,800 km ÷ 3 = 39,600 km

Worksheet

 
Chile
Mexico
U.S.A.
Date of Measurement      
Time of Measurement (local time)      
Time of Measurement (GMT)      
Latitude      
Longitude      
Gnomon height      
Shadow length      
Gnomon-sunbeam angle      

 

 
Chile-Mexico
Chile-U.S.A.
Mexico-U.S.A.
Vertical Angle      
Separation Distance
(along Zenith Circle) 		     
Earth's Circumference      
Earth's Radius